1、 任何开关电源的拓扑上电感达到稳定状态的必要条件是△Ion=△Ioff=△I

就是说开关导通阶段电流增量△Ion正好等于开关关断阶段电流减量△Ioff，只有这样电路才能达到一个稳定的状态，即使无数次重复相同的这个开关过程，每次也可以达到一样的结果;我们经常听到一个词电感复位讲的就是这个状态，满足△Ion=△Ioff就是电感复位成功。

如果说一个拓扑不能满足这个关系式，那么每个开关周期电感电流产生一个净增量，并一直累加，电流将会达到一个不可控的状态。

2、根据每次开关时电感电流的起始值不同，分为几种模式：CCM, BCM, DCM, FCCM

对电感上的电流测试，我是找了一个100mΩ的分流器放在了电感的后面，测试100mΩ电阻两端的电压

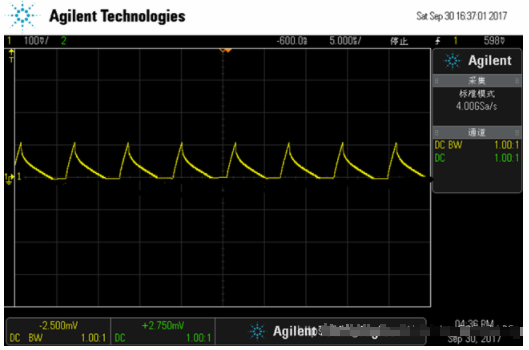
CCM:

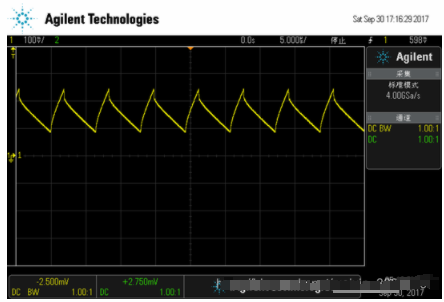
BCM:

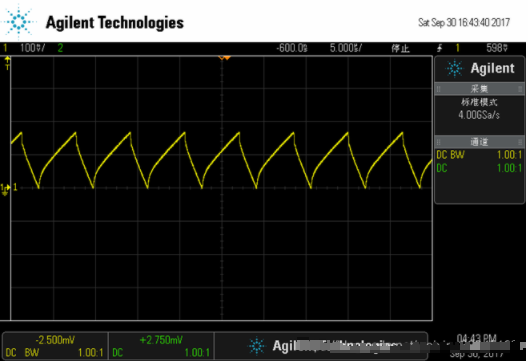
DCM:

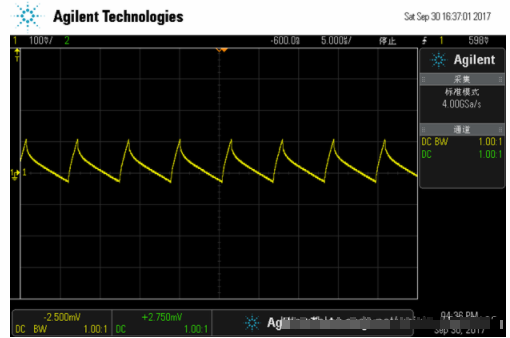
FCCM:

3、伏秒平衡

电感方程： V=L* △ I / △ T 电感两端电流连续

电感稳态时有 △ Ion= △ Ioff = △ I

由上面两个已知条件可以知道，导通阶段电感电压与导通时间的乘积一定等于关断时电感电压与关断时间的乘积，即为：

Von * Ton = Voff * Toff

这个关系式就是伏秒积平衡关系式

开关电源中占空比的定义：开关导通时间与周期之比

D=Ton/T

4、DCDC拓扑结构

Buck-boost

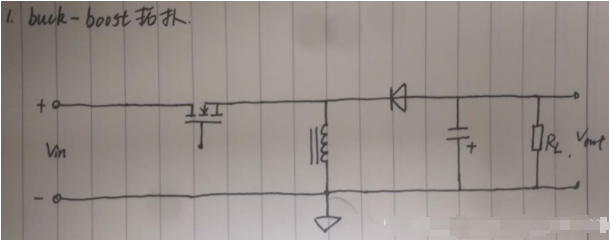
Von*Ton=Voff*Toff

Von= Vin - Vm

Voff=Vout + Vd

Toff/Ton=(Vin-Vm)/(Vout+Vd)

D=Ton/(Ton+Toff)≈Vout/(Vin+Vo)升降压的占空比计算

boost：

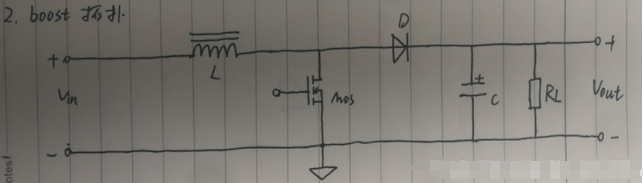
Von*Ton=Voff*Toff

Von= Vin - Vm

Voff=Vout + Vd -Vin

Toff/Ton=(Vin-Vm)/(Vout+Vd-Vin)

D=Ton/(Ton+Toff) ≈ (Vout-Vin)/Vout升压的占空比计算

buck：

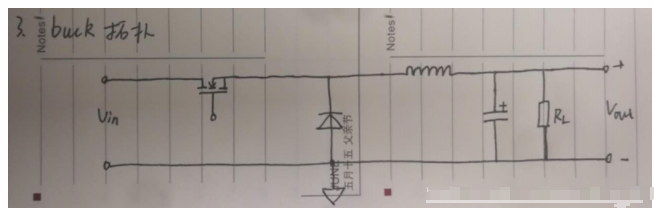
Von*Ton=Voff*Toff

Von= Vin - Vm -Vout

Voff=Vout + Vd

Toff/Ton=(Vin-Vm-Vout)/(Vout + Vd)

D=Ton/(Ton+Toff)≈Vout/Vin 降压的占空比

5、电感的计算

由电感方程：V=L*△I / △T 知道△I =V* △T /L,知道电感电流的交流纹波△I 完全由伏秒积和电感值的大小决定。

电流纹波率r：它表示的是电感电流的交流分量与直流分量比值，即r= △I / IL，这里的IL为平均直流分量

Ipk=IL

r值与电感值的关系：由△I =V* △T /L， r= △I / IL，Ton=D/f知;

r=(Von*D)/(L*IL*f)

这样也就推出：L =(Von*D)/(r*IL*f)

而且r是根据一般经验给出的，大约在0.3~0.5之间，一般就选择0.4

电感参数计算如下：

还有一个就是磁性元件常用的电流型和电压型方程

由 V=N* dΦ / dt =L*di/ dt 得到

B=L*IL/N* Ae ，电流型方程

B=U* dt /N* Ae,Bac = Uon *D/2*N* Ae *f ，电压型方程

高频变压器的计算

首先要了解磁性元件计算的两个基本定律： 1 、安培定律 2 、电磁感应定律

1. 安培定律：一个磁性均匀的环，在环的圆周上均匀绕 N 匝线圈，平均圆的周长为 Le, 线圈中通过的电流为 I, 根据全电流定律，电流与磁场强度 的关系为 I*N=H*Le 。

磁场强度 H= ( I*N ) /L e ， MKS 单位是 A/m ， GGS 的表达 H=(0.4*PI*I*N)/(100*L), 单位是奥斯特 oe 。可以看出磁场强度随着电流的增加而增加。

2. 电磁感应定律：一个 N 匝线圈，包围的面积为 A ，如果包围面积 A 中的 磁通发生变化，那么就会在线圈的两端感应出电动势，这个电动势的大小与包围面积中的磁通链的变化的关系是

U=(N* dΦ )/ dt ，其中 Φ=N*B*A ，则 U=(A*N)*dB/ dt 。

3. 联立安培定律与电磁感应定律可以得出电感的计算式。

B= μH 代入 U=(N*A)d (μ H ) / dt , 且 H=(I*N)/L ，得到 U= ( N^2*A*μ* dI ) /L* dt 。

则电感 L=(N^2*A*μ)/Le 。所以说 U=L*di/ dt 就是电磁感应定律的变形。

电感的定义：电感是导线内通过交流电流时,在导线的内部及其周围产生交变磁通,导线的磁通量与生产此磁通的电流之比. L=Φ/I