直接进入正题，如下图以Buck为例。我们首先假设，电感的电流波形以斜率m1上升，然后以斜率m2下降，在电感的电流达到峰值电流的时候限值电压（顶上的电压横线）突然受到一个干扰时间为Δt，幅值为+ΔV的干扰后（限值电压升高），电感峰值电流达到原本的峰值电流后在Δt时间内继续上升，上升的电流幅值为ΔI，随后干扰消失，电感电流以m2的斜率下降，大致如下图，下面来计算一下受到干扰后电流波形与原本的电流轨迹的差值ΔI1，ΔI2......ΔIn，是越来越大还是越来越小，越大则不稳定，越小则稳定。

上图中虚线为受到干扰后的波形，实线为原本的波形轨迹

我们把实线的第一个峰值电流记做 i1

我们把虚线的第一个峰值电流记做 i1_1

i1_1 - i1=ΔI

我们把实线的第二个峰值电流记做 i2

我们把虚线的第二个峰值电流记做 i2_1

有

i2=i2_1   i1=in_1

然后我们把时间点t1垂直建立一个坐标系，设时间轴t上的点t1为原点

可以看出i1以m2的斜率下降了时间toff，i1_1以m2的斜率下降了时间toff-Δt，可得出结论i1和i1_1下降到时间点t2后，i1_1比i1少下降了时间Δt

则i1_1比i1降低的电流为 Δt·m2

由于原来i1_1比i1就高出了ΔI    i1_1 - i1=ΔI

则如上图ΔI1=ΔI+Δt·m2

Δt是我们自己作的辅助时间线，为未知数，我们需要先把时间Δt求出

Δt和ΔI和斜率m1很容易得到关系式

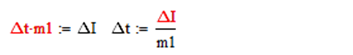
则有

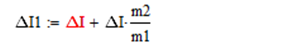
同样的方法可推导出

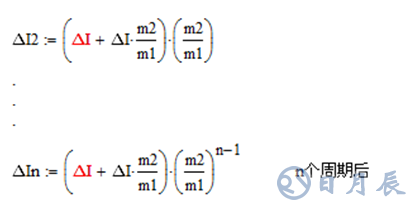
从公式非常容易得到一个结论

当m2/m1＞1时，ΔIn会越来越大，导致不稳定

然后我们假设电感电流波峰到波谷之间的电流差值为Δi（小写i）

可得到如下结论

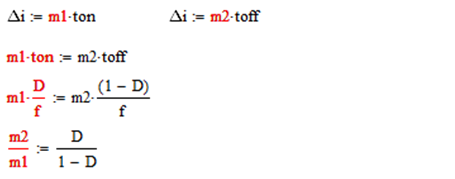
m2/m1＞1时相当于 D/(1-D)＞1，也就时相当于D＞0.5时会不稳定。

结论：Buck在不做任何处理的情况下占空比D＞0.5将导致不稳定。

下面我们分析一下，加入斜坡补偿（在限值上加入一个斜率m3）的情况

如下图所示

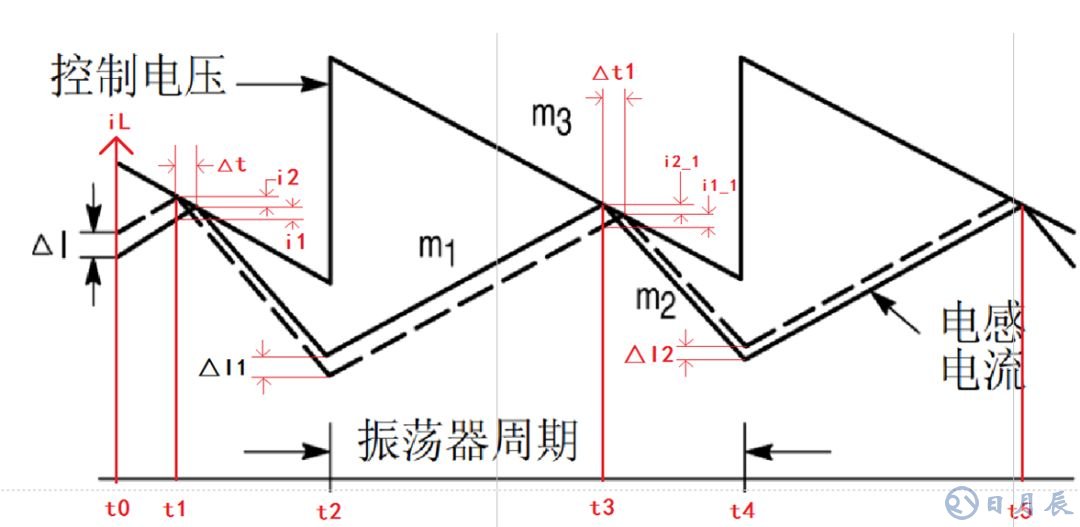
由于跟上面的分析基本类似，为了更简洁下面主要看图，尽量少用一点文字

实线和虚线到时间t2时，实线和虚线都以斜率m2下降，虚线比实线多下降了时间Δt，然后原本虚线顶点比实线顶点高出电流i2可得到

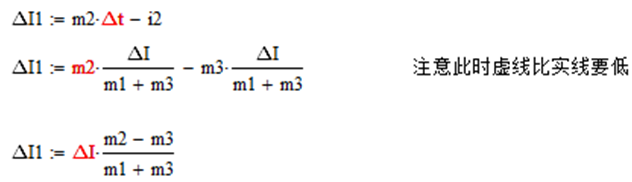
再过一个周期后，如上图

实线和虚线到时间t4时，实线和虚线都以斜率m2下降，虚线比实线少下降了时间Δt1，然后原本虚线顶点比实线顶点低出电流i2_1

可得到

根据伏秒平衡

也可以从公式中看出，D＜0.5时，系统时恒稳定的

再D＞0.5时必须满足

还可以引申一下，占空比D最大时1，我们取最大占空比1来分析

上式可变成