NMOS管，其电路模型可分为大信号模型和小信号模型。

大信号模型，是一个完整的通用的模型，其对输入交流信号没有要求;而小信号模型，使用的前提，是输入交流信号足够的小。

当VDS>VGS-VTH时，NMOS管处于饱和区，其对应的电流为：

根据ID的公式，计算ID的值：

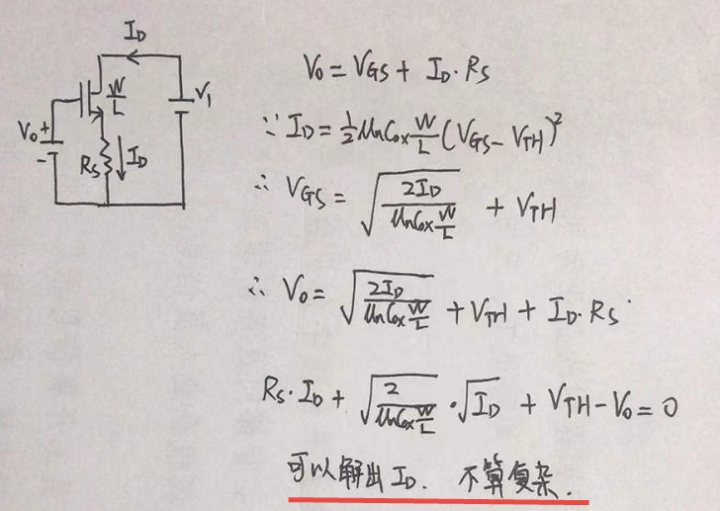
上图中，是NMOS管ID的计算，其中计算的前提，是假设V0和V1的值，使得NMOS管工作在饱和区，且忽略沟道调制效应。从上面右边的推导来看，整体还不算复杂，最后也能推导出ID的结果。

但是如果，电路变成下图所示呢?

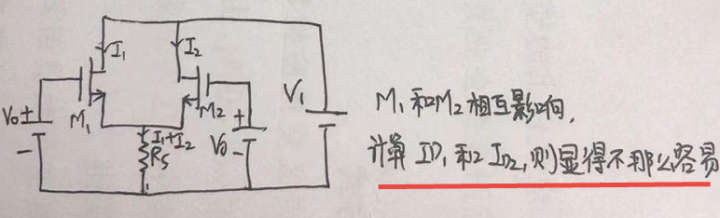
这个时候，就发现，想用确切的公式表示出ID，就显得不那么容易了。

在上述单NMOS的电路中，除了直流电压Vo外，再叠加上一个变化的信号Vs,则可以看到如下图所示的推导：

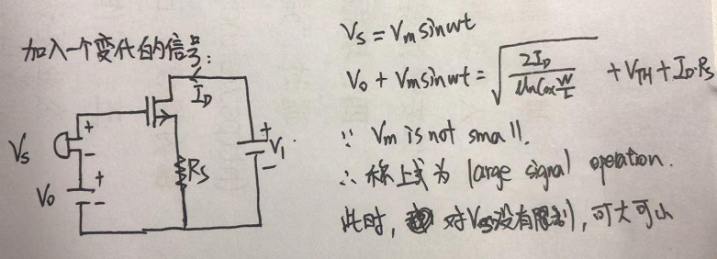
当VS不做任何限制时，则可以获得MOS管的大信号模型：

在计算偏置电流时，我们使用大信号模型;但是大信号模型并不只关乎偏置。它是一个完整通用的模型。

大信号模型虽然很完整，很通用，但是有一个致命的弱点，就是太复杂，参数多，还有非线性在上面。

幸好，当VS为小信号时，大信号模型可以进行简化，简化后的模型，被称之为小信号模型。

在推导小信号模型之前，先来看一下MOS管的另一项指标，即跨导(transconductance),gm.

gm定义如下：

也就是说，当输入电压VGS发生变化时，其输出电流ID也会发生变化。而输出电流变化量与输入电压变化量之间的比值，就称为跨导。

结合ID的电流公式，和gm的定义，即可得到gm的等式如下：

然后，再给gm做个变种。

再做个变种。

从上面的gm的三个表达式看的话，会觉得有点自相矛盾。从表达式1中，gm与VGS-VTH成正比，但到表达式2中，gm与VGS-VTH则又成反比了。这是因为，ID,VGS-VTH，W/L这三个因素通过电流公式联系在一起的。但是，在gm的表达式中，只显性表示了2个，但是还有一个因素在起作用。

比如说，对于表达式2：gm=2*ID/(VGS-VTH)而言：

(1)当ID=constant时，gm与VGS-VTH呈反比;VGS-VTH变大时，要使得ID保持不变，则需要减小W/L的值。

(2)当VGS-VTH=constant时，gm与ID成正比;ID变大时，为了使得等式依然成立，则需要提高W/L的值。

但是为什么要给gm弄出这三个公式呢，是不是以后的IC设计中会用到呢?暂时我还不知道。期待随着学习的深入，能够有答案。

知道了gm的表达式后，开始看看小信号模型的推导。

在推导之前，需要知道一个近似，即当x<<1时，(1+x)^2~=1+2*x。

对应到电路模型，则可得：

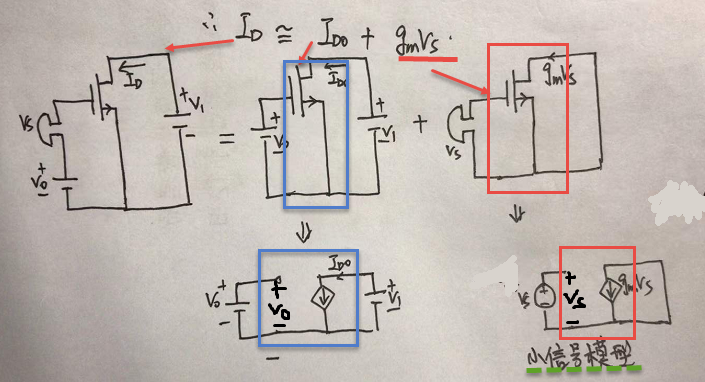
也就是说，当信号Vs很小时，大信号模型，可以分解成偏置模型和小信号模型。小信号模型反应的是变化，包括电流的变化和电压的变化。

在电路中，经常会到恒压源和恒流源，那在建立一个电路的小信号模型时，怎么处理这些源呢?

在小信号模型中，表征的是变化，即电流的变化或者电压的变化。所有不变化的，都按照零处理。

所以恒压源为0，即代表短路;恒流源为0，则代表开路。

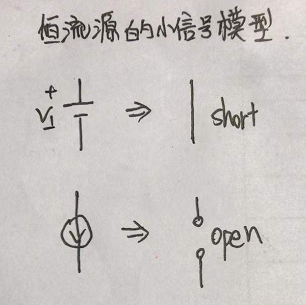
以上的小信号模型和gm的推导，都没有考虑沟道长度调制效应。

总结一下构造小信号模型的通用步骤：

(1) 给电路施加合适的偏置;

(2) 在电压上叠加小信号电压，但是一次只叠加一个。

比如上面，先使得Vo-->Vo+△V，

(3) 计算电流的变化

比如上面，ID-->ID+gm*△V

(4)用合适的电路模型来模拟这种变化，比如说用电阻，电压源，电流源等。

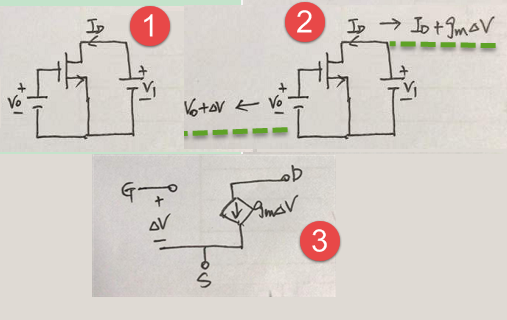
在两个端口之间施加变化的电压，但是在另外两个端口之间测量电流，需要用压控电流源来模拟;

而当电压和电流都是在同样的两端口之间的话，则可以用电阻来模拟。

那沟道长度调制效应对小信号模型又有什么影响么?

即沟道长度调制效应，使得MOS管的输出端增加了一个电阻r0.